复习课教案:基本初等函数小结
基础知识梳理:
一、幂函数
1、定义:形如![]() 的函数称为幂函数。其中
的函数称为幂函数。其中![]() 称为自变量,
称为自变量,![]() 为常数。
为常数。
2、幂函数的图像及性质
总结特征:在一象限直线![]() 右侧逆时针方向指数越来越大。
右侧逆时针方向指数越来越大。

幂函数 |
|
|
|
|
|
定义域 |
|
|
|
|
|
值域 |
|
|
|
|
|
奇偶性 |
|
|
|
|
|
单调性 |
|
|
|
|
|
公共点 |
|
|
|
|
|
二、指数函数
![]() 指数与指数幂的运算
指数与指数幂的运算
1、若![]() ,则
,则![]() 的________;若
的________;若![]() ,则
,则![]() 的________.
的________.
若![]() ,则
,则![]() 的________,用符号_________表示,其中
的________,用符号_________表示,其中![]() 叫做根式。
叫做根式。
2、根式的性质:![]()
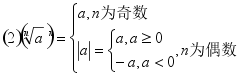
3、有理数指数幂的运算性质:![]()
![]()
![]()
![]()
![]()
![]()
4、![]() 规定正数的正分数指数幂的意义是:
规定正数的正分数指数幂的意义是:![]()
![]() 规定正数的负分数指数幂的意义是:
规定正数的负分数指数幂的意义是:![]()
![]() 0的正分数指数幂等于______,0的负分数指数幂_______.
0的正分数指数幂等于______,0的负分数指数幂_______.
5、一般地,无理数指数幂![]()
![]() 是一个___________.
是一个___________.
_____________的运算性质同样适用于无理数指数幂.
![]() 指数函数
指数函数
1、定义:一般地,函数![]() 叫做指数函数,其中
叫做指数函数,其中![]() 是自变量。
是自变量。
2、指数函数的图像与性质
|
|
|
图像 |
|
|
定义域 |
|
|
值域 |
|
|
单调性 |
|
|
定点 |
| |
图像特征 |
|
|
注意:无论在![]() 轴的右侧,还是在
轴的右侧,还是在![]() 轴的左侧,底数按逆时针方向依次变大;
轴的左侧,底数按逆时针方向依次变大;
在一象限满足底大图高;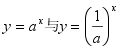 图像关于
图像关于![]() 轴对称。
轴对称。
三、应用
1、![]() ,
, ![]()
2、比较大小时,找中间值法通常选择0或1这两个数;底数相同的幂式用指数函数的单调性;底数相同的对数式用对数函数的单调性;真数相同的对数式用对数函数的图像;指数相同的幂式用幂函数的单调性或指数函数的图像。
注意:指数函数的单调性取决于底数![]() 的大小;因此解题时通常对底数
的大小;因此解题时通常对底数![]() 按
按![]() 进行分类讨论。
进行分类讨论。
3、换元时注意换元后“新元”的范围。
4、画指数函数![]() 的图像时,应抓住三个关键点
的图像时,应抓住三个关键点![]()
5、指数幂的化简问题中,首先应将根式、分数指数幂统一为,以便利用法则计算。但必须注意运算法则和运算顺序;运算结果不能同时含有根式和分数指数幂,也不能同时含有分式与负指数幂。
三、对数函数
㈠对数的概念与性质
1、对数的定义及常用对数:一般地,如果![]() ,那么数
,那么数![]() ________,记做________,其中
________,记做________,其中![]() 叫做_________,
叫做_________,![]() 叫做__________.
叫做__________.
2、常用对数是_________记为_________,自然对数是__________记为__________.
3、对数![]() 具有以下性质
具有以下性质
![]()
![]()
![]()
![]()
![]()
4、对数的运算性质![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
5、对数式与指数式![]()
| 式子 |
|
|
|
指数式 |
| 底数 |
| 幂值 |
对数式 |
|
|
|
|
![]()
1、对数函数的定义:一般地,我们把函数![]() 叫做对数函数,其中
叫做对数函数,其中![]() 是自变量,函数的定义域为
是自变量,函数的定义域为![]()
2、对数函数的图像与性质
|
|
|
图像 |
|
|
定义域 |
|
|
值域 |
|
|
单调性 |
|
|
定点 |
|
|
值域特征 |
|
|
注意:![]() 对数函数与同底的指数函数互为反函数,互为反函数的两个函数图像关于直线
对数函数与同底的指数函数互为反函数,互为反函数的两个函数图像关于直线![]() 对称,单调性相同。
对称,单调性相同。
![]() 对数函数图像在一象限与直线
对数函数图像在一象限与直线![]() 的交点分别为
的交点分别为![]() ,
,![]() ,
,![]() …,从左往右,底数
…,从左往右,底数![]() 的值越来越大。
的值越来越大。
规律方法:
1、在对数运算中,先利用幂的运算性质吧底数或真数进行变形,转化成分数指数幂的形式,使得幂的底数最简,然后用对数的运算法则化简合并。
2、先将对数式转化为同底数的对数的和、差、背书运算,然后运用对数运算法则,转化为同底数对数的积、商、幂的运算。
3、![]() 是解决有关指数、对数问题的有效方法,在运算中应注意相互转化。
是解决有关指数、对数问题的有效方法,在运算中应注意相互转化。
4、![]()
5、对一些可通过平移、对称变换能做出其图像的对数型函数,在求解其单调性、单调区间、值域、零点时,常用数形结合求解
6、利用对数函数的性质研究对数型函数的性质时,要注意以下几点:
![]() 定义域;
定义域;
![]() 底数与1的大小关系;
底数与1的大小关系;
![]() 如果需要将函数解析式变形,要确保其等价性;
如果需要将函数解析式变形,要确保其等价性;
![]() 注意复合函数由哪些基本初等函数复合而成。
注意复合函数由哪些基本初等函数复合而成。
7、对数值的大小比较法:![]() 转化为同底之后用函数的单调性;
转化为同底之后用函数的单调性;
![]() 做差或做商;
做差或做商; ![]() 利用中间值0或1;
利用中间值0或1; ![]() 化为同真数后利用图像比较。
化为同真数后利用图像比较。
8、多个对数函数图像比较底数大小的问题,可利用图像与直线![]() 交点的横坐标的大小进行判定。
交点的横坐标的大小进行判定。
典型例题:
1、设![]() ,
,![]() ,
,![]() ,则
,则![]()
![]() 、
、![]()
![]() 、
、![]()
![]() 、
、![]()
![]() 、
、![]()
2、已知函数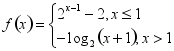 ,且
,且![]() ,则
,则![]()
![]() 、
、![]()
![]() 、
、![]()
![]() 、
、![]()
![]() 、
、![]()
3、已知![]() ,
,![]() ,
,![]() ,则
,则![]()
![]() 、
、![]()
![]() 、
、![]()
![]() 、
、![]()
![]() 、
、![]()
4、已知![]() ,
,![]() ,
,![]() ,则
,则![]()
![]() 、
、![]()
![]() 、
、![]()
![]() 、
、![]()
![]() 、
、![]()
5、用![]() 表示
表示![]() 三个数中的最小值。设
三个数中的最小值。设![]() ,
,![]() ,则
,则![]() 的最大值为
的最大值为![]()
![]() 、4
、4 ![]() 、5
、5 ![]() 、6
、6 ![]() 、7
、7
6、当![]() 时,
时,![]() ,则
,则![]() 的取值范围是
的取值范围是![]()
![]() 、
、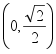
![]() 、
、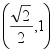
![]() 、
、 ![]()
![]() 、
、![]()
7、设![]() ,已知
,已知![]()
![]() ,则
,则![]()
![]() 、
、![]()
![]() 、
、![]()
![]() 、
、![]()
![]() 、
、 ![]()
8、已知函数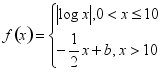 ,若
,若![]() 互不相等且
互不相等且![]() ,则
,则![]() 的取值范围是__________。
的取值范围是__________。