2021-2022年九年级中考模拟考试
数 学 试 题
一、选择题(本题有10小题,每小题4分,共40分.每小题只有一个选项是正确的,不选、多错选,均不给分)
1. ﹣2的相反数是( )
A.﹣2B.2C.﹣![]() D.
D.![]()
2我国开展了第七次全国人口普查,据国家统计局数据公布全国人口总量约为共1400000000人,数据1400000000用科学记数法表示为( )
A.14×108B.1.4×109C.1.4×1010D.0.14×1011
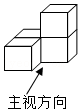
3由4个相同的正方体搭成的几何体如图所示,它的主视图是( )
A.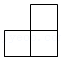 B.
B.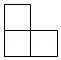
C.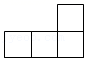 D.
D.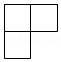
4下列计算正确的是( )
A.2x﹣x=2B.x6÷x2=x3
C.(x+y)2=x2+y2D.(﹣xy3)2=x2y6
5每年的6月5日为世界环境保护日,为提高学生环境保护意识,某校对100名学生进行“保护环境知多少”测试,抽取部分统计如下表:
成绩(分) | 60 | 70 | 80 | 90 | 100 |
人数(人) | 7 | 20 | 23 | 42 | 8 |
本次测验成绩的众数为( )
A.80分B.85分C.90分D.100分
6若反比例函数y=![]() 的图象位于第二、四象限,则k的取值范围是( )
的图象位于第二、四象限,则k的取值范围是( )
A.k<1B.k>1C.k>0D.k<0
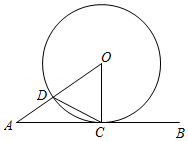
7如图,直线AB与⊙O相切于点C,AO交⊙O于点D,连接CD,OC.若∠AOC=50°,则∠ACD的度数为( )
A.20°B.25°C.30°D.35°
8《九章算术》中记录的一道题译为白话文是:把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天,如果用快马送,所需的时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间.设规定时间为x天,则可列方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9已知二次函数y=x2﹣6x+8,当0<x≤m时,﹣1≤y≤8,则m的值是( )
A.3B.4C.6D.7
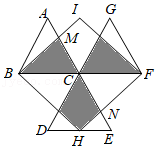
10三个大小相同的等边三角形△ABC,△CDE,△GCF按如图所示方式摆放,点A,C,E在同一直线上,且点D,C,G在同一直线上,H为DE中点,以HB、HF为邻边作▱BHFI,交AE于点M,N,若MN为8,则图中阴影部分的面积和为( )
A.![]() B.
B.![]() C.18D.36
C.18D.36
二、填空题(本题有6小题,每小题5分,共30分)
11分解因式:x2﹣6x= .
12一个不透明的袋子中装有仅颜色不同的1个红球,2个绿球和3个白球,从袋子中随机摸出一个小球,则摸出的小球恰好是一个红球概率为 .
13不等式1﹣2x≥5的解集为 .
14已知圆锥的底面半径为4cm,母线长为5cm,则这个圆锥的侧面积是 .
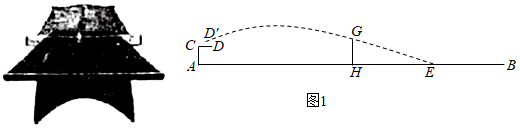
15某校购买了一套乒乓球桌和自动发球机,侧面如图1所示,球台长度AB=274cm,发球机紧贴球台端线点A处,高出球台的部分AC=12cm,出球管道CD=5![]() cm,若将水平状态的CD绕点C逆时针旋转45°到CD的位置,发球机模式为“一跳球”,路线呈抛物线,离球台正中间的球网GH左侧72cm处到达最高点高出台面21cm,则EB= cm.
cm,若将水平状态的CD绕点C逆时针旋转45°到CD的位置,发球机模式为“一跳球”,路线呈抛物线,离球台正中间的球网GH左侧72cm处到达最高点高出台面21cm,则EB= cm.
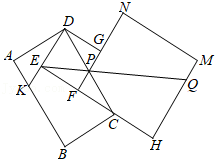
16矩形ABCD的面积记为S1、正方形DEFG的面积记为S2、正方形FHMN的面积记为S3,它们的位置如图所示,点C在FH上,FG交CD于点P,延长DE交AB于点K,AD=2AK=6,点B,C,M在同一直线上,则![]() = ;若S1+S2=S3,射线EP交HM于点Q,则QM的长为 .
= ;若S1+S2=S3,射线EP交HM于点Q,则QM的长为 .
三、解答题(本题有8小题。共80分.解答需写出必要的文字说明、演算步骤或证明过程)
17(1)计算:![]() ﹣(
﹣(![]() )﹣1+|﹣5|.
)﹣1+|﹣5|.
(2)化简:![]() ﹣
﹣![]() .
.
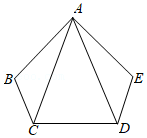
18已知:如图,在五边形ABCDE中,AB=AE,∠B=∠E,BC=ED.
(1)求证:△ABC≌△AED.
(2)当AC∥DE,∠ADE=40°时,求∠ACD的度数.
19某商家对A、B两款学生手表的销售情况进行了为期五个月的调查统计,期间两款手表的月销售量统计图如图所示.
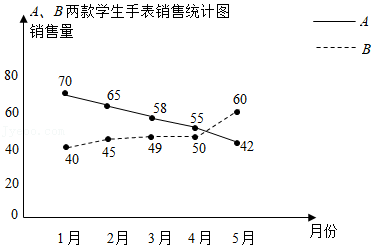
(1)请求出A款学生手表这五个月的总销售量以及B款学生手表4月﹣5月的销售量增长率;
(2)参考这五个月的销售情况,请对这两款手表未来的进货、销售方面提出你的建议.
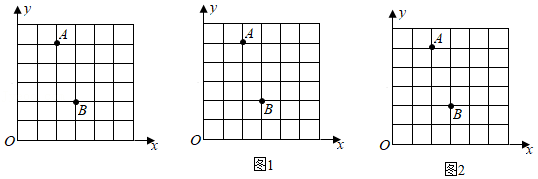
20在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的平行四边形为整点平行四边形.如图,已知整点A(2,5),B(3,2),请在所给网格区域内按要求画以A,B,C,D为顶点的整点平行四边形.
(1)在图1中画出点C,D,使点C的横、纵坐标之和等于点D的横、纵坐标之和的3倍;
(2)在图2中画出点C,D,使点C的横、纵坐标之积等于点D的横、纵坐标之积的2倍.
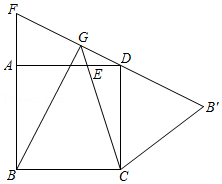
21如图,抛物线y=﹣x2+bx+c(b>0),交x轴于点A、B,交y轴于点C,已知A的横坐标为﹣1.
(1)求点B的坐标.(用含b的代数式表示)
(2)抛物线的对称轴交x轴于点D,连结BC,平移线段CB,使点C与D重合,此时点B恰好落在抛物线上,求b的值.
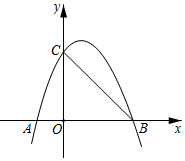
22如图,AC是⊙O的直径,四边形ABCD是⊙O的内接四边形,点E在![]() 上,DE⊥BC于点F,DE交AC于点G,且∠CDF=∠ACB.
上,DE⊥BC于点F,DE交AC于点G,且∠CDF=∠ACB.
(1)求证:四边形ABEG是平行四边形.
(2)若AC=25,CD=24,求EG的长.
23某厂家生产甲,乙两款机器人,为测试机器人性能,两机器人在同一起点出发,沿直线跑道上匀速行走,两款机器人上都有实时统计步数的显示器(机器人每走1步,显示器上步数累计加1).已知甲,乙机器人的步距分别为0.4m,0.5m(步距是指每一步的距离),运动过程中的时刻和步数如下:
| 出发时刻 | 出发时显示器中已显示的步数 | 9:05时显示器中显示的步数 |
甲 | 9:00 | 170 | a |
乙 | 9:00 | 220 | a |
已知当9:05时,乙比甲多走了5m.
(1)求表中a的值.
(2)9:05后,甲机器人按原速度继续沿直线行走,乙机器人再行走t分钟后(t为整数)往回走(转身时间忽略不计),相遇时两机器人同时停止行走.
①现计划乙机器人往回走的路程不超过10m,求t的最大值.
②为保证9:11时两机器人恰好相遇,将乙每分钟步数增加m步,求相遇时乙机器人显示器上显示的步数.
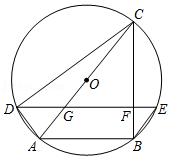
24如图,已知E为正方形ABCD的边AD上一点,连结CE,点B关于CE的对称点为B'连结B'D,并延长B'D交BA的延长线于点F,延长CE交B′F于点G,连结BG.
(1)求证:∠CBG=∠CDB′.
(2)若AE=2DE,BC=6,求BG的长.
(3)在(2)的条件下,H为直线BG上一点,过点H作CG的平行线l.当直线l恰好经过△ADF的顶点时,求BH的长.
2021年浙江省温州市鹿城区中考数学二调试卷
一、选择题(本题有10小题,每小题4分,共40分.每小题只有一个选项是正确的,不选、多错选,均不给分)
1. ﹣2的相反数是( )
A.﹣2B.2C.﹣![]() D.
D.![]()
【考点】相反数.
【答案】B
【分析】根据一个数的相反数就是在这个数前面添上“﹣”号,求解即可.
【解答】解:﹣2的相反数是:﹣(﹣2)=2,
故选:B.
2我国开展了第七次全国人口普查,据国家统计局数据公布全国人口总量约为共1400000000人,数据1400000000用科学记数法表示为( )
A.14×108B.1.4×109C.1.4×1010D.0.14×1011
【考点】科学记数法—表示较大的数.
【专题】实数;数感.
【答案】B
【分析】用科学记数法表示较大的数时,一般形式为a×10n,其中1≤|a|<10,n为整数,,且n比原来的整数位数少1.
【解答】解:1400000000=1.4×109.
故选:B.
3由4个相同的正方体搭成的几何体如图所示,它的主视图是( )

A. B.
B.
C. D.
D.
【考点】简单组合体的三视图.
【专题】投影与视图;空间观念.
【答案】A
【分析】根据简单组合体三视图的画法,画出其主视图即可.
【解答】解:该组合体的主视图如下:

故选:A.
4下列计算正确的是( )
A.2x﹣x=2B.x6÷x2=x3
C.(x+y)2=x2+y2D.(﹣xy3)2=x2y6
【考点】合并同类项;幂的乘方与积的乘方;同底数幂的除法;完全平方公式.
【专题】整式;运算能力.
【答案】D
【分析】根据合并同类项法则判断A,根据同底数幂的除法的运算法则判断B,根据完全平方公式判断C,根据积的乘方的运算法则判断D.
【解答】解:A、2x﹣x=x,原计算错误,故此选项不符合题意;
B、x6÷x2=x4,原计算错误,故此选项不符合题意;
C、(x+y)2=x2+2xy+y2,原计算错误,故此选项不符合题意;
D、(﹣xy3)2=x2y6,原计算正确,故此选项符合题意.
故选:D.
5每年的6月5日为世界环境保护日,为提高学生环境保护意识,某校对100名学生进行“保护环境知多少”测试,抽取部分统计如下表:
成绩(分) | 60 | 70 | 80 | 90 | 100 |
人数(人) | 7 | 20 | 23 | 42 | 8 |
本次测验成绩的众数为( )
A.80分B.85分C.90分D.100分
【考点】众数.
【专题】数据的收集与整理;数据分析观念.
【答案】C
【分析】根据众数的定义,出现次数最多的数为众数.
【解答】解:这组数据中90出现次数最多,
所以这组数据的众数为90,
故选:C.
6若反比例函数y=![]() 的图象位于第二、四象限,则k的取值范围是( )
的图象位于第二、四象限,则k的取值范围是( )
A.k<1B.k>1C.k>0D.k<0
【考点】反比例函数的性质.
【答案】A
【分析】由反比例函数所在的象限可得到关于k的不等式,可求得答案.
【解答】解:
∵反比例函数y=![]() 的图象位于第二、四象限,
的图象位于第二、四象限,
∴k﹣1<0,解得k<1,
故选:A.
7如图,直线AB与⊙O相切于点C,AO交⊙O于点D,连接CD,OC.若∠AOC=50°,则∠ACD的度数为( )

A.20°B.25°C.30°D.35°
【考点】垂径定理;圆周角定理;切线的性质.
【专题】与圆有关的位置关系;推理能力.
【答案】B
【分析】先根据切线的性质得到∠OCA=90°,再根据等腰三角形的性质和三角形内角和计算出∠OCD=65°,然后计算∠OCA﹣∠OCD即可.
【解答】解:∵直线AB与⊙O相切于点C,
∴OC⊥AB,
∴∠OCA=90°,
∵OC=OD,
∴∠OCD=∠ODC=![]() (180°﹣∠COD)=
(180°﹣∠COD)=![]() ×(180°﹣50°)=65°,
×(180°﹣50°)=65°,
∴∠ACD=∠OCA﹣∠OCD=90°﹣65°=25°.
故选:B.
8《九章算术》中记录的一道题译为白话文是:把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天,如果用快马送,所需的时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间.设规定时间为x天,则可列方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【考点】由实际问题抽象出分式方程.
【专题】分式方程及应用;应用意识.
【答案】A
【分析】首先设规定时间为x天,则快马所需的时间为(x﹣3)天,慢马所需的时间为(x+1)天,由题意得等量关系:慢马速度×2=快马速度,根据等量关系,可得方程.
【解答】解:设规定时间为x天,则快马所需的时间为(x﹣3)天,慢马所需的时间为(x+1)天,由题意得:
![]() ×2=
×2=![]() ,
,
故选:A.
9已知二次函数y=x2﹣6x+8,当0<x≤m时,﹣1≤y≤8,则m的值是( )
A.3B.4C.6D.7
【考点】二次函数的性质.
【专题】二次函数图象及其性质;运算能力;应用意识.
【答案】C
【分析】根据题目中的函数解析式和二次函数的性质,可以得到该函数的对称轴和开口方向,再根据当0<x≤m时,﹣1≤y≤8和二次函数具有对称性,可以得到m的值.
【解答】解:∵二次函数y=x2﹣6x+8=(x﹣3)2﹣1,
∴该函数的对称轴是直线x=3,函数图象开口向上,当x=3时取得最小值﹣1,
∵当0<x≤m时,﹣1≤y≤8,当x=0时,y=8,当x=6时,y=8,
∴m=6,
故选:C.
10三个大小相同的等边三角形△ABC,△CDE,△GCF按如图所示方式摆放,点A,C,E在同一直线上,且点D,C,G在同一直线上,H为DE中点,以HB、HF为邻边作▱BHFI,交AE于点M,N,若MN为8,则图中阴影部分的面积和为( )

A.![]() B.
B.![]() C.18D.36
C.18D.36
【考点】全等三角形的判定与性质;等边三角形的性质;平行四边形的性质.
【专题】图形的相似;运算能力;推理能力.
【答案】A
【分析】如图,连接IC,过点M作MR⊥BF于R.设BC=CF=m.想办法求出BF,IC,根据阴影部分的面积=△IBF的面积,求解即可.
【解答】解:如图,连接IC,CH,过点M作MR⊥BF于R.设BC=CF=m.
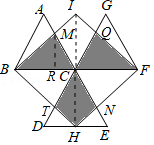
∵等边三角形△ABC,△CDE,△GCF全等,点A,C,E在同一直线上,且点D,C,G在同一直线上,
∴∠FCE=∠CED=60°,
∴DE∥BF,
∵CD=CE,DH=HE,
∴CH⊥DE,
∴CH⊥BF,
∵BC=CF,
∴HB=HF,
∵四边形BHFI是平行四边形,
∴四边形BHFI是菱形,
∴IB=IF,
∵BC=CF,
∴IC⊥BF,
∵IC=![]() m,
m,
∴tan∠IBC=![]() =
=![]() ,
,
∵CM=CN=4,∠RMC=90°,∠MCR=60°,
∴RC=![]() CM=2,RM=
CM=2,RM=![]() CR=2
CR=2![]() ,
,
∵![]() =
=![]() ,
,
∴BR=4,
∴BC=CF=6,CI=3![]() ,
,
由对称性可知,阴影部分的面积=△IBF的面积=![]() •BF•IC=
•BF•IC=![]() ×12×3
×12×3![]() =18
=18![]() ,
,
故选:A.
二、填空题(本题有6小题,每小题5分,共30分)
11分解因式:x2﹣6x= .
【考点】因式分解﹣提公因式法.
【答案】见试题解答内容
【分析】首先找出公因式,进而提取公因式得出答案.
【解答】解:x2﹣6x=x(x﹣6).
故答案为:x(x﹣6).
12一个不透明的袋子中装有仅颜色不同的1个红球,2个绿球和3个白球,从袋子中随机摸出一个小球,则摸出的小球恰好是一个红球概率为 .
【考点】概率公式.
【专题】概率及其应用;数据分析观念.
【答案】![]() .
.
【分析】用红色球的个数除以球的总个数即可.
【解答】解:∵袋子中共有1+2+3=6个除颜色外其它都相同的球,其中红球有1个,
∴从袋子中随机摸出一个小球,摸出的球是红球的概率是![]() ,
,
故答案为:![]() .
.
13不等式1﹣2x≥5的解集为 .
【考点】解一元一次不等式.
【专题】一元一次不等式(组)及应用;运算能力.
【答案】x≤﹣2.
【分析】移项、合并同类项,系数化成1即可求解.
【解答】解:移项得﹣2x≥5﹣1,
合并同类项得﹣2x≥4,
系数化为1得x≤﹣2,
故答案为:x≤﹣2.
14已知圆锥的底面半径为4cm,母线长为5cm,则这个圆锥的侧面积是 .
【考点】圆锥的计算.
【专题】计算题.
【答案】见试题解答内容
【分析】根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式计算.
【解答】解:这个圆锥的侧面积=![]() •2π•4•5=20π(cm2).
•2π•4•5=20π(cm2).
故答案为20πcm2.
15某校购买了一套乒乓球桌和自动发球机,侧面如图1所示,球台长度AB=274cm,发球机紧贴球台端线点A处,高出球台的部分AC=12cm,出球管道CD=5![]() cm,若将水平状态的CD绕点C逆时针旋转45°到CD的位置,发球机模式为“一跳球”,路线呈抛物线,离球台正中间的球网GH左侧72cm处到达最高点高出台面21cm,则EB= cm.
cm,若将水平状态的CD绕点C逆时针旋转45°到CD的位置,发球机模式为“一跳球”,路线呈抛物线,离球台正中间的球网GH左侧72cm处到达最高点高出台面21cm,则EB= cm.

【考点】二次函数的应用.
【专题】二次函数的应用;应用意识.
【答案】(209﹣30![]() ).
).
【分析】以AC为y轴,以AB为x轴,A为原点建立平面直角坐标系,设抛物线最高点为N,对称轴MN与x轴交于M,则MN=21,根据题意写出抛物线解析式y=a(x﹣65)2+21(a<0),然后通过旋转求出D′坐标,再把D′坐标代入抛物线求出a,再令y=0解一元二次方程求出E对岸坐标即可.
【解答】解:以AC为y轴,以AB为x轴,A为原点建立平面直角坐标系,如图,
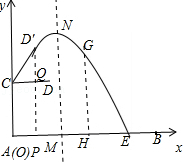
设抛物线最高点为N,对称轴MN与x轴交于M,则MN=21,
∴AB=274cm,
∵GH是AB正中间,
∴AH=![]() AB=137cm,
AB=137cm,
∴AM=AH﹣MH=137﹣72=65cm,
设抛物线为:y=a(x﹣65)2+21(a<0),
过D′作D′P⊥x轴交CD于点Q,交x轴于点P,
则∠CQD′=∠APQ=90°,
∵旋转45°,
∴CD′=CD=5![]() cm,
cm,
CQ=D′Q=CD′cos∠D′CD=5cm,
∴D′P=D′Q+PQ=5+12=17cm,
∴D′(5,17)代入抛物线得:
a×(5﹣65)2+21=17,
∴a=﹣![]() ,
,
∴y=﹣![]() (x﹣65)2+21,
(x﹣65)2+21,
令y=0,则﹣![]() (x﹣65)2+21=0,
(x﹣65)2+21=0,
解得:x1=65+30![]() ,x2=65﹣30
,x2=65﹣30![]() (舍去),
(舍去),
∴E(65+30![]() ,0),
,0),
∴EB=AB﹣AE=274﹣(65+30![]() )=(209﹣30
)=(209﹣30![]() )(cm),
)(cm),
故答案为:(209﹣30![]() ).
).
16矩形ABCD的面积记为S1、正方形DEFG的面积记为S2、正方形FHMN的面积记为S3,它们的位置如图所示,点C在FH上,FG交CD于点P,延长DE交AB于点K,AD=2AK=6,点B,C,M在同一直线上,则![]() = ;若S1+S2=S3,射线EP交HM于点Q,则QM的长为 .
= ;若S1+S2=S3,射线EP交HM于点Q,则QM的长为 .

【考点】全等三角形的判定与性质;矩形的性质;正方形的性质.
【专题】图形的全等;矩形 菱形 正方形;推理能力.
【答案】![]() ;
;![]() .
.
【分析】先推出∠ADK=∠GDP,可得![]() =
=![]() =
=![]() ,再证明△DPG≌△CPF,进而证明
,再证明△DPG≌△CPF,进而证明![]() =
=![]() =
=![]() ,HF=2CF=2DG,即可得
,HF=2CF=2DG,即可得![]() =
=![]() ;设DE=x,则EC=FH=HM=2x,DC=
;设DE=x,则EC=FH=HM=2x,DC=![]() =
=![]() =
=![]() x,列出方程,求出x的值,再证明
x,列出方程,求出x的值,再证明![]() =
=![]() =
=![]() ,进而可求出QM的长.
,进而可求出QM的长.
【解答】解:如图,连结CM,
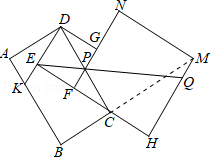
在矩形ABCD、正方形DEFG中,∠ADC=∠EDG=90°,
∴∠ADC﹣∠EDP=∠EDG﹣∠EDP,
即∠ADK=∠GDP,
∴tan∠ADK=tan∠GDP,
∵AD=2AK,
即![]() =
=![]() =
=![]() ,
,
∴PG=![]() DG=
DG=![]() FG,
FG,
∴PG=FP,
在△DPG和△CPF中,
 ,
,
∴△DPG≌△CPF(ASA),
∴DG=CF,
∴DE=DG=EF=CF,
即CE=2DE,
∵点B,C,M在同一直线上,
∴∠DCM=180°﹣90°=90°,
∴∠DCE+∠MCH=∠MCH+∠CHM=90°,
∴∠DCE=∠CMH,
∴tan∠DCE=tan∠CMH,
∴![]() =
=![]() =
=![]() ,
,
∴HM=HF=2CH,
∴HF=2CF=2DG,
∴![]() =
=![]() =
=![]() ,
,
设DE=x,则EC=FH=HM=2x,
∴DC=![]() =
=![]() =
=![]() x,
x,
∴FH=HM=4![]() ,
,
∵S1+S2=S3,AD=6,
∴6×![]() x+x2=(2x)2,
x+x2=(2x)2,
解得,x=2![]() 或x=0(舍去),
或x=0(舍去),
∴EH=EF+FH=x+2x=3x=6![]() ,
,
∵PF垂直平分EC,
∴PE=PC,
∴∠PEC=∠PCE=∠PDG=∠ADK,
∴tan∠PEC=tan∠ADK,
即![]() =
=![]() =
=![]() ,
,
∴QH=![]() EH=3
EH=3![]() ,
,
∴QM=HM﹣QH=4![]() ﹣3
﹣3![]() =
=![]() .
.
故答案为:![]() ;
;![]() .
.
三、解答题(本题有8小题。共80分.解答需写出必要的文字说明、演算步骤或证明过程)
17(1)计算:![]() ﹣(
﹣(![]() )﹣1+|﹣5|.
)﹣1+|﹣5|.
(2)化简:![]() ﹣
﹣![]() .
.
【考点】实数的运算;分式的加减法;负整数指数幂.
【专题】实数;分式;运算能力.
【答案】(1)2![]() +3;
+3;
(2)![]() .
.
【分析】(1)原式利用二次根式性质,负整数指数幂法则,以及绝对值的代数意义计算即可求出值;
(2)原式通分并利用同分母分式的减法法则计算,约分即可得到结果.
【解答】解:(1)原式=2![]() ﹣2+5
﹣2+5
=2![]() +3;
+3;
(2)原式=![]() ﹣
﹣![]()
=![]()
=![]()
=![]() .
.
18已知:如图,在五边形ABCDE中,AB=AE,∠B=∠E,BC=ED.
(1)求证:△ABC≌△AED.
(2)当AC∥DE,∠ADE=40°时,求∠ACD的度数.

【考点】全等三角形的判定与性质.
【专题】证明题;图形的全等;推理能力.
【答案】(1)证明过程见解答;
(2)70°.
【分析】(1)利用SAS即可证明结论;
(2)结合(1)可得AC=AD,根据等腰三角形的性质即可求出∠ACD的度数.
【解答】(1)证明:在△ABC和△AED中,
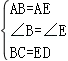 ,
,
∴△ABC≌△AED(SAS);
(2)解:∵AC∥DE,∠ADE=40°,
∴∠CAD=∠ADE=40°,
∵△ABC≌△AED,
∴AC=AD,
∴![]() .
.
19某商家对A、B两款学生手表的销售情况进行了为期五个月的调查统计,期间两款手表的月销售量统计图如图所示.

(1)请求出A款学生手表这五个月的总销售量以及B款学生手表4月﹣5月的销售量增长率;
(2)参考这五个月的销售情况,请对这两款手表未来的进货、销售方面提出你的建议.
【考点】折线统计图.
【专题】统计的应用;应用意识.
【答案】(1)A款手表这五个月的总销售量为290只,B款4月﹣5月的销售量增长率为20%;(2)见解析.
【分析】(1)根据统计图中的数据把A款学生手表这五个月的销售量相加得A款学生手表这五个月的总销售量,根据B款学生手表4月、5月的销售量可得增长率;
(2)根据折线统计图所给出的数据,提出合理的建议即可.
【解答】解:(1)A款手表这五个月的总销售量:70+65+58+55+42=290(只),
B款4月﹣5月的销售量增长率:![]() ;
;
(2)答案不唯一.从销售量来看,B款手表销售量逐月上升,5月份超过了A款手表销售量,建议多进B款手表,少进或不进A款手表;从总销售量来看,由于A款手表逐月减少,导致总销售量减少,建议采取一些促销手段,增加A款手表的销售量.
20在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的平行四边形为整点平行四边形.如图,已知整点A(2,5),B(3,2),请在所给网格区域内按要求画以A,B,C,D为顶点的整点平行四边形.
(1)在图1中画出点C,D,使点C的横、纵坐标之和等于点D的横、纵坐标之和的3倍;
(2)在图2中画出点C,D,使点C的横、纵坐标之积等于点D的横、纵坐标之积的2倍.

【考点】坐标与图形性质;平行四边形的性质;作图—复杂作图.
【专题】作图题;几何直观.
【答案】(1)(2)作图见解析部分.
【分析】(1)利用数形结合的思想以及题目要求作出图形即可.
(2)利用数形结合的思想以及题目要求作出图形即可.
【解答】解:(1)如图,四边形ACBD即为所求.
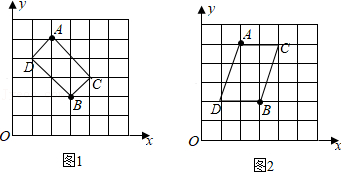
(2)如图,四边形ACBD即为所求.
21如图,抛物线y=﹣x2+bx+c(b>0),交x轴于点A、B,交y轴于点C,已知A的横坐标为﹣1.
(1)求点B的坐标.(用含b的代数式表示)
(2)抛物线的对称轴交x轴于点D,连结BC,平移线段CB,使点C与D重合,此时点B恰好落在抛物线上,求b的值.
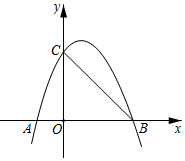
【考点】二次函数的性质;二次函数图象上点的坐标特征;抛物线与x轴的交点;坐标与图形变化﹣平移.
【专题】二次函数图象及其性质;推理能力.
【答案】(1)(b+1,0).
(2)![]() .
.
【分析】(1)先求出图象对称轴为直线x=![]() ,再通过点A坐标(﹣1,0)求出点B坐标.
,再通过点A坐标(﹣1,0)求出点B坐标.
(2)先求出点D坐标,然后由平移线段CB,使点C与D重合得出点B坐标,将点B坐标代入解析式求解.
【解答】(1)∵y=﹣x2+bx+c,
∴对称轴为直线![]() ,
,
∴![]() ,
,
∵A点横坐标为﹣1,
∴B(b+1,0).
(2)对称轴直线x=![]() 与x轴交点为(
与x轴交点为(![]() ,0),
,0),
把A(﹣1,0)代入y=﹣x2+bx+c,
得:﹣1﹣b+c=0,即c=b+1,
∵平移线段CB,使C与D重合点,
∴B平移后得点![]() ,
,
∵点B在抛物线上,
∴![]() ,
,
解得![]() ,
,
∵b>0,
∴![]() .
.
22如图,AC是⊙O的直径,四边形ABCD是⊙O的内接四边形,点E在![]() 上,DE⊥BC于点F,DE交AC于点G,且∠CDF=∠ACB.
上,DE⊥BC于点F,DE交AC于点G,且∠CDF=∠ACB.
(1)求证:四边形ABEG是平行四边形.
(2)若AC=25,CD=24,求EG的长.

【考点】勾股定理;平行四边形的判定与性质;垂径定理;圆周角定理;圆内接四边形的性质;相似三角形的判定与性质.
【专题】综合题;数形结合;等腰三角形与直角三角形;多边形与平行四边形;圆的有关概念及性质;几何直观.
【答案】(1)见解答过程.
(2)15.
【分析】(1)直径所对的圆周角是直角,可得DE∥AB,通过角度转化可得∠CGE=∠BEG,可得AC∥BE,平行四边形可证.
(2)AC为直径,△ADC是直角三角形,勾股定理可得AC,求得∠ACB正切值,可求AB,继而可求EG.
【解答】解(1)证明:∵AC为直径,
∴∠ABC=90°,
∵CD⊥BC,
∴EG∥AB.
∵∠CDF=∠ACB,
∴∠FGC=∠DCF,
∵∠DCF=∠DEB,
∴∠DEB=∠FGC,
∴AG∥BE
∴四边形ABEG是平行四边形.
(2)解:如图,
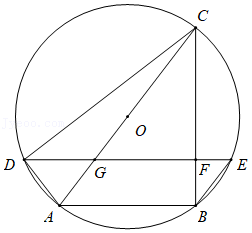 ,
,
在Rt△ADC中,AC=25,CD=24,
∴AD=![]() =7,
=7,
∵四边形ABEG是平行四边形,
∴∠AGD=∠BED,DE∥AB,AD=BE,AB=EG,
∴∠AGE=∠BED,
∴∠ADG=∠AGD.
∴AD=AG=BE=7,
∵∠CDF=∠ACB,∠CFD=∠CFD,
∴△CDF∽△GCF,
∴![]() ,
,
∵DE∥AB,
∴△CGF∽△CAB,
∴![]() =
=![]() ,
,
在Rt△ABC中,设AB=3a,则BC=4a,
∴(3a)2+(4a)2=252,
解得a=5,
∴AB=15
∴EG=15.
23某厂家生产甲,乙两款机器人,为测试机器人性能,两机器人在同一起点出发,沿直线跑道上匀速行走,两款机器人上都有实时统计步数的显示器(机器人每走1步,显示器上步数累计加1).已知甲,乙机器人的步距分别为0.4m,0.5m(步距是指每一步的距离),运动过程中的时刻和步数如下:
| 出发时刻 | 出发时显示器中已显示的步数 | 9:05时显示器中显示的步数 |
甲 | 9:00 | 170 | a |
乙 | 9:00 | 220 | a |
已知当9:05时,乙比甲多走了5m.
(1)求表中a的值.
(2)9:05后,甲机器人按原速度继续沿直线行走,乙机器人再行走t分钟后(t为整数)往回走(转身时间忽略不计),相遇时两机器人同时停止行走.
①现计划乙机器人往回走的路程不超过10m,求t的最大值.
②为保证9:11时两机器人恰好相遇,将乙每分钟步数增加m步,求相遇时乙机器人显示器上显示的步数.
【考点】列代数式;一元一次方程的应用.
【专题】行程问题;一次方程(组)及应用;模型思想.
【答案】(1)470;
(2)14;
(3)1304步.
【分析】(1)根据表格表示出甲机器人走了(a﹣170)步,乙机器人走了(a﹣220)步,根据“当9:05时,乙比甲多走了5m.”列出方程即可求解;
(2)①设乙往回走x米,甲,乙各走了(![]() +t)分钟,则甲要走24(
+t)分钟,则甲要走24(![]() +t)米,乙往前走了25t米,根据乙机器人往回走的路程不超过10m,求出t的最大值;
+t)米,乙往前走了25t米,根据乙机器人往回走的路程不超过10m,求出t的最大值;
②设乙往回走了(6﹣t)分钟,根据相遇列出方程,根据m和t都是整数求解.
【解答】解:(1)由题意得,甲机器人走了(a﹣170)步,乙机器人走了(a﹣220)步,
∴0.4(a﹣170)+5=0.5(a﹣220),解得a=470;
(2)由(1)得,甲每分钟走60×0.4=24米,乙每分钟走50×0.5=25米,
设乙往回走x米,甲,乙各走了(![]() +t)分钟,则甲要走24(
+t)分钟,则甲要走24(![]() +t)米,乙往前走了25t米,
+t)米,乙往前走了25t米,
∴24(![]() +t)﹣5+x=25t,
+t)﹣5+x=25t,
即t=![]() x﹣5,
x﹣5,
∵x≤10,
∴t≤14.6,
∴t最大为14;
(3)设乙往回走了(6﹣t)分钟,
∴6×24﹣5+0.5(50+m)(6﹣t)=(50+m)×0.5t,
即m=![]() =﹣50+
=﹣50+![]() ,
,
∵m和t是整数,
∴t=4,m=89,
∴6×(50+89)+470=1304(步).
24如图,已知E为正方形ABCD的边AD上一点,连结CE,点B关于CE的对称点为B'连结B'D,并延长B'D交BA的延长线于点F,延长CE交B′F于点G,连结BG.
(1)求证:∠CBG=∠CDB′.
(2)若AE=2DE,BC=6,求BG的长.
(3)在(2)的条件下,H为直线BG上一点,过点H作CG的平行线l.当直线l恰好经过△ADF的顶点时,求BH的长.

【考点】四边形综合题.
【专题】几何综合题;推理能力.
【答案】见试题解答内容
【分析】(1)根据对称性以及等腰三角形的性质只能即可.
(2)如图1中,连结BB'交CG于点M,证明BG=![]() BM,即可解决问题.
BM,即可解决问题.
(3)直线l经过△ADF三个顶点时,有三种情况:①如图2,直线l经过点A时,交BB'于点N,交BC于点K,②如图3,当直线l经过点D时,过点G作AD的平行线交l于点P,则四边形EDPG是平行四边形,③如图3,当直线l经过点F时,过点C作CQ⊥BG于点Q,分别求解,可得结论.
【解答】(1)证明:如图1中,
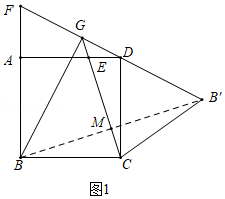
∵点B与B'关于CG对称,
∴∠CBG=∠B',B'C=BC,
∴B'C=CD,
∴∠B'=∠CDB',
∴∠CBG=∠CDB'.
(2)解:如图1中,连结BB'交CG于点M,
∵∠CDG+∠CDB'=180°,
∴∠CDG+∠CBG=180°,
∴∠BCD+∠BGB'=180°,
∵∠BCD=90°,
∴∠BGB'=90°,
∵BG=B'G,
∴![]() ,
,
∵∠DCE+∠MCB=∠MCB+∠MBC,
∴∠ECD=∠CBM,
∴![]() ,
,
∴![]() ,
,
∴BG=![]() BM=
BM=![]() .
.
(3)解:在Rt△CBM中,CM=![]() =
=![]() =
=![]() ,
,
∴![]() ,
,
直线l经过△ADF三个顶点时,有三种情况:
①如图2,直线l经过点A时,交BB'于点N,交BC于点K,
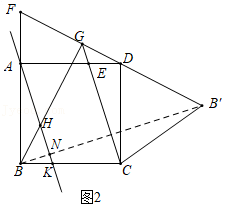
∵AK∥EC,AE∥CK,
∴四边形AECK是平行四边形,
∴AE=CK,
∵AD=BC,
∴DE=BK,
∵∠ABK=∠CDE=90°,AB=CD,
∴△ABK≌△CDE(SAS),
∴BK=DE,
∵![]() ,
,
∴![]() .
.
②如图3,当直线l经过点D时,过点G作AD的平行线交l于点P,则四边形EDPG是平行四边形,
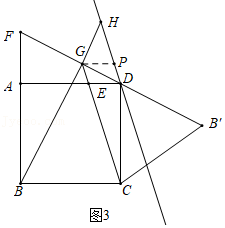
∴PG=DE=2,由△GPH∽△BCG,可得![]() ,
,
∴![]() ,
,
∴![]() .
.
③如图3,当直线l经过点F时,过点C作CQ⊥BG于点Q,
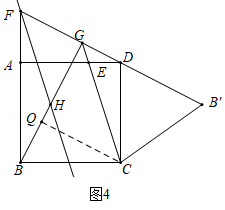
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
综上所述,![]() 或
或![]() 或
或![]() .
.
数学中考试题 第 1 页